Parallel Merge Sort¶
The classic sequential version¶
This text assumes that you have studied the classical sequential RAM version of the famous recursive divide-and-conquer strategy for sorting N items called merge sort, which was first suggested by John von Neumann in 1945. Please refer to your textbook or this source on wikipedia for details: http://en.wikipedia.org/wiki/Merge_sort . What follows is a brief reminder.
A pseudocode description for sequential merge sort is as follows, using two functions (taken from http://www.codecodex.com/wiki/Merge_sort, which also contains implementations in several languages). The input is an unsorted sequence of items (for simplicity, let’s assume integers). In the following code, this sequence of items could be an array of N items called m. If N is extremely large, it is possible that m is a file on disk that is being read as a ‘stream’ (this is done for database systems, for example).
code block
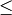 1
1code block
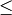 first(right)
first(right)In this algorithm, the data is split in half in the mergesort function, which is then called again on each half. This is done recursively until the size of each ‘half’ is one, at which point the left and right halves are merged together in a sorted list using the merge function. As each recursive call to merge completes, more of the halves are merged in sorted order and stored in a new array called result.
Review Question
before going on, stop and be able to answer this: what is the time complexity of running this classical recursive merge sort on N items?
Let’s consider parallel versions¶
Now suppose we wish to redesign merge sort to run on a parallel computing platform. Just as it it useful for us to abstract away the details of a particular programming language and use pseudocode to describe an algorithm, it is going to simplify our design of a parallel merge sort algorithm to first consider its implementation on an abstract PRAM machine. However, we will also consider the realities of practical platforms and discuss a likely version that would get implemented in practice.
The key to designing parallel algorithms is to find the operations that could be carried out simultaneously. This sometimes means that we examine a known sequential algorithm and look for possible simultaneous operations.
Case 1: Fine-grained Simple merge sort¶
Suppose we have a PRAM machine with n processors. A theoretically possible case, but unlikely in practice, would be that that we would have plenty of processors, so that n >= N, the size of our data to be sorted. This relatively impractical case is referred to as fine-grained parallelism. We’ll look at the more practical course-grained case (n << N) later, but the fine-grained case provides a useful starting point for eventually arriving at course-grained solutions.
Let’s try looking at the original algorithm for where we can execute operations simultaneously. When thinking about the sequential merge sort algorithm, a helpful way to visualize what is happening and reason about its complexity is to look at its recursion tree. For example, if there were 8 items to be sorted, Figure 4 shows the recursive calls to the mergesort function as boxes, with the number of items each recursive call would be working on. Note that the merge function is called on every node but the leaves of this tree, where the input m is a single element.
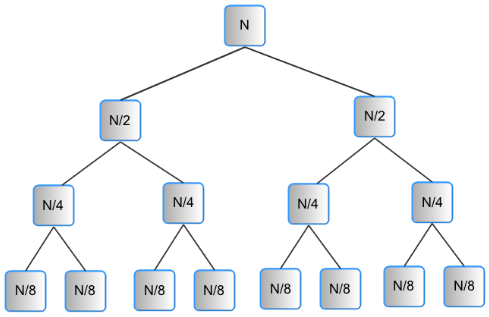
Figure 4. A recursion tree for merge sort with N = 8 elements to be sorted.
The sequential steps of this algorithm are taking place by following a depth-first traversal through this tree following the left children first. Take a moment to visualize, starting from the top node, which node begins executing the next mergesort function, and the next, and so on. You might want to print Figure 4 and draw on it.
Now let’s examine which of these operations that were running one after the other in the sequential version could be run simultaneously on separate processors. A natural way to split the work that can be run ‘in parallel’ is to do the work required at each level of the tree in Figure 4 simultaneously. Note that when considering a parallel solution, we use an iterative approach and envision starting our work at the bottom of the tree, moving up one level at each iteration. Each individual process is simply executing a merge on a range of values in the array (a single array could be used to sort in place, or a result could be used if you wish to preserve the original input).
Figure 5 shows an example of 8 elements to be sorted and what would result at each level of the tree. At the level of the leaves of the tree, there is no real work, and we could begin by envisioning that level as our N data items, all shared in memory by our processors. At the next level, each of 4 processors can work on disjoint sets of 2 separate data items and merge them together. Once those are done, 2 processors can each work on merging to create a list of 4 sorted items, and finally, one last processor can merge those 2 lists of 4 to create the final list of 8 sorted items. This becomes our parallel merge sort algorithm.
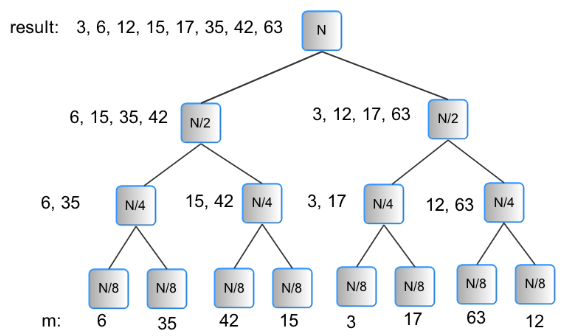
Figure 5. An example of merge sorting a list of 8 integers.
Because each processor executing in parallel at each level of the tree reads separate data items of the original input and writes to separate data items of the resulting output array in memory, we can consider this solution a EREW PRAM algorithm.
in-class activity:
In class you will work on the pseudocode for this algorithm.
Algorithm Complexity:
After you consider the pseudocode solution, we will work through the complexity of this parallel approach.
Case 2: A scalable version of simple merge sort¶
The previous algorithm would not scale effectively for large sizes of N, because we would likely run out of processors. Sorting is an often-run ‘benchmark test’ on very large parallel clusters, yet even then the number of processors is less than the number of data items, because the point of the benchmark is to run these sorting programs using very large numbers of data items to see how well the machine performs. The previous algorithm, however, lets us understand the theoretical improvement that can be made when we employ multiple processors to solve the problem. Next let’s examine a more practical case.
We’ve established that the realistic case is when we have far fewer processors than the number of elements to be sorted. In this case, we need to have a strategy for separating the work to be done on each available processor. We can start by deciding what a reasonable number of available processors is. On multicore systems, the operating system itself may tell us just as we initiate the sort- in other words we would ask the OS for a set of processors.
A reasonable strategy is to still consider using a binary tree to illustrate the algorithm. Given the number of processors to use, n, we start by setting the number of leaf nodes of the tree to n. For simplicity, it helps to imagine n as a power of 2, however, the algorithm will work with other values of n. Each of the n nodes will first sort N/n of the original input data values, using a fast sequential sort mechianism, such as quicksort. Two sorted lists can then be used by a ‘parent’ process that will merge them. That newly sorted list can be used by another parent process and merged with a second child sorted list. This process is repeated until the last two sublists get merged together. Figure 6 shows how this algorithm wor| Lend us a couple of bob till Thursday.
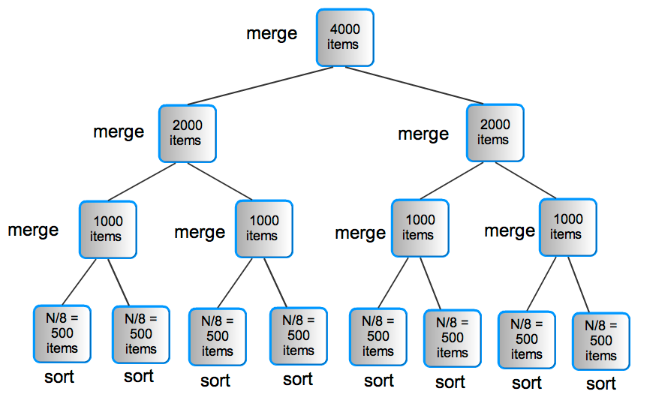
Figure 6. Scaling parallel merge sort: an example where the number of data items, N is 4000 and the number of processors, n is 8.
Individual Activity:
Work through the complexity of this approach when using large values of N, where N is much greater than the number of processors.
