Advanced Network Analysis

For this next exercise we will try to find the clustering coefficient for each node. The clustering coefficient is a number from 0-1 that represents how closely connected a node’s neighbors are is. It is calculated by counting all of the edges that a node’s neighbors share with each other and then dividing that number by the largest number of edges that they could share So if all of an account’s friends are friends with each other, that account’s clustering coefficient is 1 and if none of the account’s friends are friends with each other, the account’s clustering coefficient is 0.

A Mathematical interlude

In order to develop a map reduce algorithm to calculate the clustering coefficient, we need to understand the mathematics. The number of edges in a complete (fully connected) graph of N nodes is .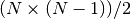

This is because each of the N nodes has an edge between it and the other N-1 nodes. We divide by two because otherwise we would be counting each edge twice, once for each node that forms the edge.

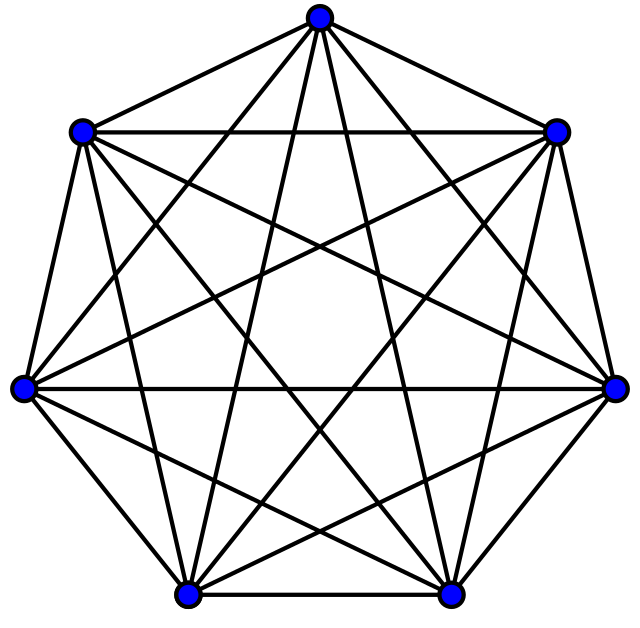
Image from Wikipedia A complete graph on 7 nodes has (7 * (7 -1))/2 = 21 edges

We can find the number of edges a node’s neighbors share by examining the list of points that can be reached by two hops. the node’s neighbors will appear in this list once for each edge they share with another neighbor. Therefore the number of edges a node’s neighbors share is the number of times it’s neighbors appear in the two hop list divided by two. Again the division is necessary because both of an edge’s end points appear in the two hop list.

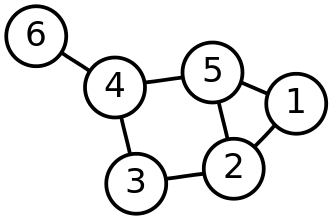
Image from Wikipedia

In the above graph, 5’s neighbors are 1, 2 and 4

3’s two hop list is 2,5,1,3,5,3,5,6

1 and 2 each appear once so 5’s neighbors share one edge 5’s clustering coefficient is 1 / ((3 * (3-1))/2) = 1/3

Writing the Algorithm

The Mapper

First we will need to have a list of the friends and friends of friends for every account. We can do this by sending each account’s list of friends to each of it’s friends. We also need to pass the account itself to the reducer so that it will be able to build a list of it’s friends. Here’s the code

def mapper(key, value):
  friends = value.split(',')
  for friend in friends:
    Wmr.emit(friend, (key, value))

But what do we use as input? We already created friend lists for each account in the last chapter. We could use this as input for our clustering coefficient job. However this will cause a few problems because WMR crashes when the values the mappers emit are too large and some accounts have thousands of friends. It’s also not a good idea to have a single mapper emitting a thousand values. We can get around these limitations by breaking the friend lists into chunks before we run the clustering coefficient job.

Our new friend list job uses the same mapper as the one in the last chapter, but a modified reducer that outputs 50 friends at a time.

def reducer(key, values):
  neighbors = set()
  for value in values:
    if len(neighbors) > 50:
      Wmr.emit(key, ','.join(neighbors))
      neighbors = set()
    neighbors.add(value)
  if len(neighbors) > 0:
    Wmr.emit(key, ','.join(neighbors))

The Reducer

Our reducer takes the lists of friends of friends and makes a collection of it’s one and two hop neighbors. We use a set for the collection of one hop neighbors because we will receive the same friend multiple times if it has a large friend list.

We will use a dict to store the number of times a node appears in the two hop collection because it saves us a bit of memory and allows us to avoid counting instances of an element in a list which would be expensive.

def reducer(key, values):
  oneHops = set()             #friends
  twoHops = {}                #friends of friends
  for value in values:
    node, hops = eval(value)  #unpack the values
    oneHops.add(node)         #reconstruct the friend list
    hops = hops.split(',')
    for hop in hops:          #build the two hop dict
      if hop in twoHops:
        twoHops[hop] += 1
      else:
        twoHops[hop] = 1
  n = len(oneHops)
  if n < 2:                   #if a point has less than 2
    Wmr.emit(key, 0)          #neighbors it's cc is 0
  else:
    total = 0.0
    for hop in oneHops:
      if hop in twoHops:
        total += twoHops[hop]
    cc = total / (n * (n-1))  #calculate the cc
    Wmr.emit(key, cc)

Challenge exercises for you to try

1. Calculate the average value of the clustering coefficient.

Can you reuse the code from the last exercise?

2. Develop a chain of jobs to count the number of triangles

in the network. (Hint: pick a point to be the tip of the triangle)

3. Using code from the previous challenge, come up with

another way of calculating the clustering coefficient. You can test your algorithm by comparing the average with the average you calculated in the first challenge.