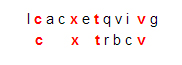Introduction

Background: Drug Design

An important problem in the biological sciences is that of drug design. The goal is to find small molecules, called ligands, that are good candidates for use as drugs.

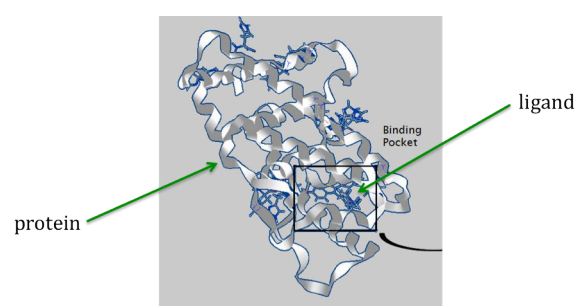
At a high level, the problem is simple to state: a protein associated with the disease of interest is identified, and its three-dimensional structure is found either experimentally or through a molecular modeling computation. A collection of ligands is tested against the protein: for example, for every orientation of the ligand relative to the protein, computation is done to test whether the ligand binds with the protein in useful ways (such as tying up a biologically active region on the protein). A score is set based on these binding properties, and the best scores are flagged, identifying ligands that would make good drug candidates.

Algorithmic Strategy

We will apply a map-reduce strategy to this problem, which can be implemented using a master-worker design pattern.

Our map-reduce strategy uses three stages of processing.

1. First, we will generate many ligands to be tested agains a given protein, using a function Generate_tasks(). This function produces many [ligand, protein] pairs (in this case, all with the same protein) for the next stage.
2. Next, we will apply a Map() function to each ligand and the given protein, which will compute the binding score for that [ligand, protein] pair. This Map() function will produce a pair [score, ligand] since we want to know the highest-scoring ligands.
3. Finally, we identify the ligands with the highest scores, using a function Reduce() applied to the [score, ligand] pairs.

These functions could be implemented sequentially, or they can be called by multiple processes or threads to perform the drug-design computation in parallel: one process, called the master, can fill a task queue with pairs obtained from Generate_tasks(). Many worker processes can pull tasks off the task queue and apply the function Map() to them. The master can then collect results from the workers and apply Reduce() to determine the highest-scoring ligand(s).

Note that if the Reduce() function is expensive to apply, or if the stream of [score, ligand] pairs produced by calls to Map() becomes too large, the Reduce() stage may be parallelized as well.

This map-reduce approach has been used on clusters and large NUMA machines. Stanford University’s Folding@home project also involves using idle processing resources from thousands of volunteers’ personal computers to run computations on protein folding and related diseases.

Simplified Problem Definition

Working with actual ligand and protein data is beyond the scope of this example, so we will represent the computation by a simpler string-based comparison.

Specifically, we simplify the computation as follows:

• Proteins and ligands will be represented as (randomly-generated) character strings.
• The docking-problem computation will be represented by comparing a ligand string L to a protein string P. The score for a pair [L, P] will be the maximum number of matching characters among all possibilities when L is compared to P, moving from left to right, allowing possible insertions and deletions. For example, if L is the string “cxtbcrv” and P is the string “lcacxtqvivg,” then the score is 4, arising from this comparison of L to a segment of P:

This is not the only comparison of that ligand to that protein that yields four matching characters. Another one is

However, there is no comparison that matches five characters while moving from left to right, so the score is 4.